Matriks - Aljabar Linier


Assalamualaikum Wr. Wb. Halo semua! Saya Faisal Indrianto, mahasiswa mata kuliah Aljabar Linear Universitas Narotama akan membahas salah satu bab aljabar linear. Namun sebelum itu, mari kita berkenalan dulu apa itu aljabar linear dan matriks. Ikuzo!

Aljabar linear adalah bidang studi matematika yang mempelajari sistem persamaan linear dan solusinya, vektor, serta transformasi linear. Dan kali ini saya akan membahas salah satu bagian dari aljabar linier yaitu matriks. Matriks dan operasinya juga merupakan hal yang berkaitan erat dengan bidang aljabar linear.

Matriks adalah susunan sekelompok bilangan dalam suatu jajaran berbentuk persegi panjang yang diatur berdasarkan baris dan kolom dan diletakkan antara dua tanda kurung. Tanda kurung yang digunakan untuk mengapit susunan anggota matriks tersebut dapat berupa tanda kurung biasa atau tanda kurung siku. Setiap bilangan pada matriks disebut elemen (unsur) matriks. Kumpulan elemen yang tersusun secara horizontal disebut baris. Sedangkan kumpulan elemen yang tersusun secara vertikal disebut kolom.

contoh matriks

Matriks sendiri memiliki ordo, ordo adalah bilangan yang menunjukkan banyaknya baris dan kolom dalam suatu matriks.

ordo matriks

Bentuk Matriks

Matrik memiliki berbagai macam bentuk, berikut macam macam bentuk matriks.

1. Matrik Nol
Matriks Nol adalah matriks yang semua elemennya bernilai nol.
Contoh Matriks Nol

2.  Matriks Skalar
Matriks skalar adalah matriks yang elemen-elemen diagonal utamanya sama, sedangkan yang lain bernilai nol.
Contoh Matriks Skalar
3. Matriks Identitas
Matriks identitas adalah matriks persegi yang nilai elemen-elemen diagonalnya adalah 1.
Contoh Matriks Identitas
4.  Matriks Diagonal
Matriks diagonal adalah matriks yang elemen-elemen diluar diagonal utamanya nol.
Contoh Matriks Diagonal



5.  Matriks Segitiga Atas
Matriks  segitiga atas adalah matriks bujur sangkar yang elemen-elemen di bawah diagonal utamanya (kiri atas ke kanan bawah) bernilai nol.

Contoh Matriks Segitiga Atas

Operasi

2 atau lebih matriks juga dapat diberikan suatu operasi :

1. Operasi Penjumlahan dan Pengurangan
Dua buah matriks dapat dijumlahkan jika memiliki ordo yang sama.






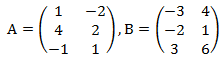
Tentukan A+B!



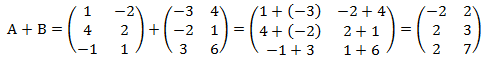
2. Operasi Perkalian

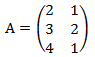
Tentukan 3A!



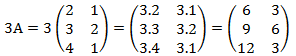
dan berikut contoh perkalian 2 matriks :


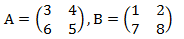
Tentukan AB




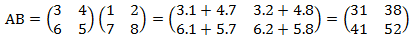
Transpos

Matriks juga dapat di transposkan, berikut tentang transpos matriks :

Matriks A transpos (At) adalah sebuah matriks yang disusun dengan cara menuliskan baris ke-i matriks A menjadi kolom ke–i dan sebaliknya.

Contoh : 

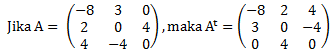
Beberapa sifat matriks adalah sebagai berikut : 
  1. (A + B)t = At + Bt
  2. (At)t = A
  3. (cA)t = cAt, c adalah konstanta
  4. (AB)t = BtAt

Determinan

Determinan dari matriks A dinotasikan dengan |A|


Jika Berordo 2×2, menentukan determinannya:


Jika berordo 3×3 menggunakan kaidah Sarrus



Sumber :
https://id.wikibooks.org/wiki/Subjek:Matematika/Materi:Matriks
https://rumushitung.com/2014/07/24/rumus-matriks-matematika-sma/
https://aimprof08.wordpress.com/2015/12/06/metode-sarrus/
http://www.allmipa.com/2016/06/determinan-matriks-dengan-berbagai-ordo.html

Komentar

Posting Komentar

Postingan populer dari blog ini

Program Menghitung Invers Matriks Menggunakan Javascript

Gambar
Assalamualaikum Wr. Wb. Selamat malam semua. Kali ini saya membuat sebuah program untuk menghitung invers dari suatu matriks. Program ini ditujukan untuk tugas dari mata kuliah Aljabar Linier. Program ini saya buat menggunakan HTML, CSS, dan library Javascript populer bernama jQuery. Program 100% original buatan dan ketikan jari jari saya (yhaa sedikit nyontek dari documentation jQuery untuk syntax Javascriptnya, h3h3) Langsung saja, berikut demo dari programnya (bisa juga download source codenya dari link berikut) :  Codepen Screenshot Program Source Code : See the Pen Inverse Matrix with jQuery by Faisal Indrianto ( @faisal-indrianto ) on CodePen .
Baca selengkapnya

HABIB BIN ZAID

Gambar
HABIB BIN ZAID LAMBANG KECINTAAN DAN PENGORBANAN                  Pada bai’at ‘Aqabah ke-II yang telah Sering kita sebut-sebut, di mana 70 orang laki-laki dan dua orang wanita mengangkat bai’at kepada Rasulullah saw. maka Habib bin Zaid dan bapaknya Zaid bin ‘Ashim termasuk 70 orang yang turut mengambil bagian . . . . Ibunya yang bernama Nusaibah binti Ka’ab me­rupakan salah seorang dari dua wanita pertama yang bai’at kepada Rasulullah tersebut sedang satunya lagi ialah bibinya saudara dari ibunya Habib bin Zaid …. Dengan demikian Habib adalah seorang Mu’min dari ang­katan lama, di mana keimanan telah menjalari persendian sampai ke tulang sumsumnya. Dan semenjak hijrahnya Nabi ke Madinah, ia selalu berada di sampingnya tak pernah ketinggalan dalam suatu peperangan dan tidak pula melalaikan suatu kewajiban …. Pada suatu ketika, di selatan jazirah Arab muncullah dua pimpinan pembohong durjana yang ...
Baca selengkapnya

Perangkat Lunak Komputer

    Perangkat keras atau hardware pada suatu komputer tidak akan bisa berjalan maksimal tanpa sebuah perangkat lunak atau software. Sebuah hardware yang canggih akan berfungsi bila perintah-perintah tertentu diberikan kepadanya, perintah-perintah tersebut diberikan melalui sebuah perangkat lunak.     Pengertian Software komputer adalah sekumpulan data elektronik yang disimpan dan diatur oleh komputer, data elektronik yang disimpan oleh komputer itu dapat berupa program atau instruksi yang akan menjalankan suatu perintah. Melalui sofware atau perangkat lunak inilah suatu komputer dapat menjalankan suatu perintah. Jenis-jenis Software atau Perangkat Lunak    Software atau perangkat lunak komputer berdasarkan distribusinya dibedakan menjadi beberapa macam, yaitu software berbayar, software gratis atau free ( Freeware, free software, shareware, adware) . Software Berbayar    Software berbayar merupakan perangkat lunak yang didi...
Baca selengkapnya